応力とひずみ

中尾です。2回目のコラムになります。

今回は、「応力」と「ひずみ」について話をします。この2つは、機械特性もしくは力学特性を表現する重要な物理量です。極めて重要な物理量ですが、よほどのことがない限り、大学になって初めて習う物理量です。しかし、理工系のほぼ全ての学科で学ぶことになる物理量です。なぜ、高校生までで教えないのでしょうか？

物体に力を加えると、その力は物体の中で分散します。例えば、２つの柱に両端を支えられた板の真ん中に荷重をかけると、板全体が曲がることと一緒です。高校の物理で習うように、物体の重心や負荷した点だけで力をささえている訳ではありません。実際には、板の例で挙げたように、物体が少しずつ連続的に形を変えて（＝「変形」と呼びます。）、荷重を物体全体で分散しています。

物体が力や変形を分散させることができるのは、物体が多数の原子の集合体であるからです。原子と原子は、化学結合で連結されています。（分子と分子もしくは結晶と結晶の間も化学結合で連結されています。材料によっては、分子間の関係で説明した方が、理解が容易な場合もありますが、今回は、原子間の相関で話を進めます。）これらの無数の化学結合がすこしずつ伸び縮みすることを連鎖的に生じることで、物体としての変形を表現します。

化学結合の結合力を大別すると、図1に示すように、結合されている原子（もしくはイオン）の間に働く、万有引力と静電気力から成る引力成分と自身の占有体積を保持するために働く斥力成分からなります。そして、通常は、引力成分と斥力成分が等しくなる距離に原子と原子が保たれることになります。ここで、物体を引張って物体を引き延ばすことを考えましょう。こうすると、化学結合が伸びることになるため、その化学結合は安定な原子間距離から大きくなり、化学結合の結合力は引張成分が大きくなります。これは、物体が引き延ばされたことへの反応として、化学結合が元の長さに戻ろうとする反発力を発生させていることになります。物体を押し縮めた場合は、その逆のことが生じます。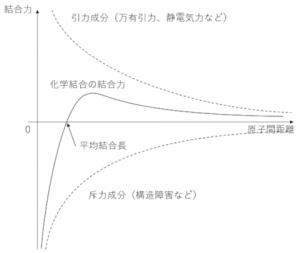

「応力」とは、この変形に対する化学結合の反発力の単位面積当たりの総和をとったものです。実際には、物体内には無数の原子が存在しており、それらの原子が連携して変形に反応しているため、取り扱いを容易にするために、単位面積当たりで規格化されています。

また、「ひずみ」とは、化学結合が伸び縮みされた距離を安定な原子間距離で規格化することで、変形の度合いを表す物理量としたものとなります。

「応力」や「ひずみ」を計算したり、取り扱う際には、Wikipediaなどでも説明されているようなマクロな視点からのアプローチを用いた方が簡単ではあります。しかし、「材料学」を勉強する君たちは、是非とも、今回のコラムのようなミクロな視点から定義を覚えておいてください。

[このコラムからの課題]

・Wikipediaの「応力」、「ひずみ」の定義、説明を調べ、マクロな視点から説明とミクロな視点からの説明で大きく異なる点を指摘し、説明せよ。